1. 概念
之前的介绍过查找二叉树,在原始数据为有序序列的时候,建立的查找二叉树跟链表别无两样。由于这种情况下的查找二叉树完全倾斜,其平均查找时间和最坏查找时间都是O(n),显然效率很低。
究其原因,查找二叉树没有有效的机制来维持其的平衡性。我们用平衡因子来表示一个结点左子树和右子树的高度之差,若这个值的绝对值始终不大于1,则称这种查找二叉树树为AVL树,即平衡二叉树。
显然查找二叉树若是完全的,则它是一种AVL树。
2. 维护平衡性原理
在插入数据的过程中,当某个结点的平衡因子出现绝对值大于1的情况时,需要通过对原来的二叉树进行旋转操作来维持其性质,根据不同的情况,分成了4中不同的旋转方式:LL,RR,LR,RL,具体解释如下:
以离新插入结点最近的祖先结点为准
- LL:新结点Y被插入到A的左子树的右子树上
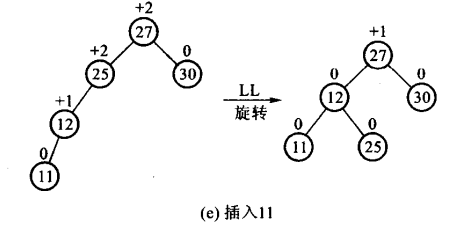
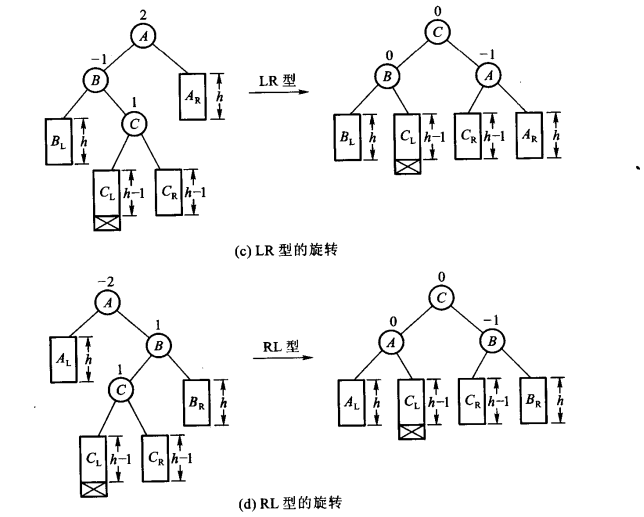
- LR:新结点Y被插入到A的左子树的右子树上

- RR:新结点Y被插入到A的右子树的右子树上
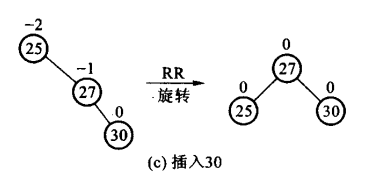
- RL:新结点Y被插入到A的右子树的左子树上
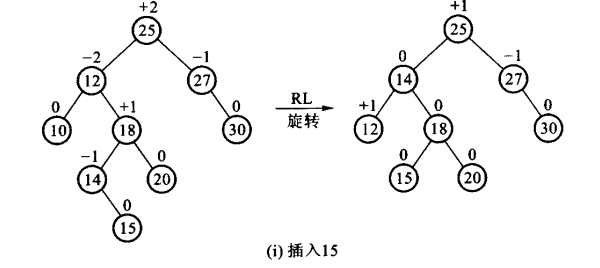
对于四种旋转方式的具体描述:
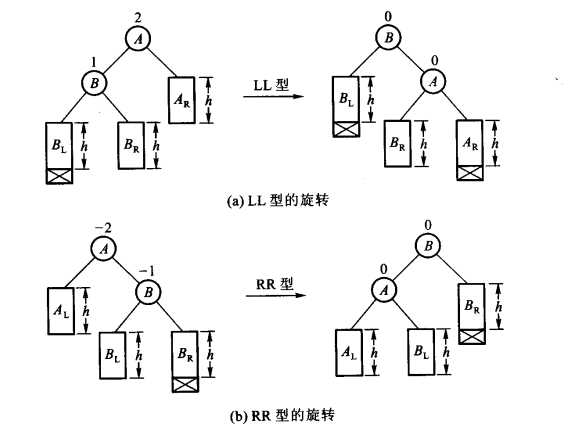
3. 代码实现
- 定义AVL树的类型:
int unbalanced = FALSE; struct node { records data; int bf; node *lchild; node *rchild; }; typedef node * AVL; - 实现LL与LR旋转
void LeftRotation(AVL &T, int &unbalanced) { AVL gc,lc; lc = T->lchild; if(lc->bf == 1) { T->lchild = lc->rchild; lc->rchild = T; T->bf = 0; T = lc; } else { gc = lc->rchild; lc->rchild = gc->lchild; gc->lchild = lc; T->lchild = gc->rchild; gc->rchild = T; switch(gc->bf) { case 1: T->bf = -1; lc->bf = 0; break; case 0: T->bf = lc->bf = 0; break; case -1: T->bf = 0; lc->bf = 1; } T = gc; } T->bf = 0; unbalanced = FALSE; } 实现RR和RL旋转则和前面类似,大家自己解决吧
插入数据
void AVLInsert(AVL &T,records R,int &unbalanced) { if(!T) { unbalanced = TRUE; T = new celltype; T->data = R; T->lchild = T->rchild = NULL; T->bf = 0; } else if (R.key < T->data.key) { AVLInsert(T->lchild,R,unbalanced); if(unbalanced) { switch(T->bf) { case -1: T->bf = 0; unbalanced = FALSE; break; case 0: T->bf = 1; break; case 1: LeftRotation(T,unbalanced); } } } else if (R.key > T->data.key) { AVLInsert(T->rchild,unbalanced); if(unbalanced) { case 1: T->bf = 0; unbalanced = FALSE; break; case 0: T->bf = -1; break; case -1: RightRotation(T,unbalanced); } } else unbalanced = FALSE; } - 删除操作(代码类似,自己写)
分三种情况:
(1)需要删除的节点下并没有其他子节点。
(2)需要删除的节点下有一个子节点(左或右)。
(3)需要删除的节点下有两个子节点(既左右节点都存在)。
对于第三种情况,则要想办法替换其左子树的最右结点(和二叉查找树刚好相反)